Fiches d'Exercices sur le Sens du Nombre

Il y a quelques affiches de numéros différents dans cette section. Les deux premières, sur le thème des oiseaux et des papillons, présentent différentes façons de représenter les nombres de 0 à 9. Deux versions des chiffres sont utilisées pour montrer les différents styles d'impressions, une version en braille et une version dans la langue des signes américaine sont également inclues pour sensibiliser les élèves aux différentes façons de représenter chaque chiffre. Une représentation linéaire et une représentation à dix images suivent, puis une représentation picturale utilisant le thème. Les chiffres de la taille d'une affiche sont faits pour être imprimés et affichés dans votre classe ou votre école.

Dans la section "écrire les chiffres et les nombres jusqu'à 20" vous trouverez que la version A des fiches d'exercices comprend tous les chiffres, les versions B à E ont environ la moitié des chiffres inclus, les versions F à I ont environ un tiers des chiffres inclus et la version J ne comprend aucun chiffre... seulement les lignes sur lesquelles les écrire. Toutes les versions comprennent des tirets sous les numéros, de sorte que les élèves ont une référence pour savoir où placer les numéros. Vous pouvez accéder aux autres versions (B à J) une fois que vous avez sélectionné la version A que vous souhaitez ci-dessous.

Ces fiches d'exercices sur le comptage par bonds comprennent des représentations visuelles des objets que l'élève est en train de compter. Par exemple, dans la fiche d'exercice "Compter par 3", les élèves verront des groupes de trois voitures. Cela permet aux élèves de développer une image mentale du comptage par bonds. Avec des nombres plus importants, l'inclusion de groupes d'éléments devient peu pratique, de sorte que les nombres sont plutôt imprimés sur les voitures.

Cent graphiques sont utiles non seulement pour apprendre à compter, mais aussi pour de nombreuses autres utilisations en mathématiques. Par exemple, un tableau de cent peut être utilisé pour modéliser des fractions et pour convertir des fractions en décimales. Pour modéliser un quart de tableau sur cent, il faudrait colorier un carré sur quatre. Après avoir colorié un carré sur quatre, on obtient 25 carrés colorés, soit 25/100 ou 0,25. Pas de magie, juste des mathématiques. Les tableaux de cent peuvent également être utilisés comme papier millimétré pour faire des graphiques, apprendre les longues multiplications et divisions ou pour tout autre usage. Une utilisation courante de cent tableaux dans les classes plus anciennes est de s'en servir pour trouver des nombres premiers et des nombres composés en utilisant le tamis d'Eratosthène.

Les grilles de 120 sont très similaires aux grilles de 100, sauf qu'elles comportent les chiffres de 101 à 120. 120 est un bon chiffre pour de nombreuses raisons. L'une d'entre elles est qu'il comporte beaucoup de diviseurs - 16 en fait. Le nombre 120 est donc utile pour de nombreuses activités de regroupement. Une deuxième raison est que le nombre 120 comprend quelques nombres à trois chiffres qui pourraient être une bonne introduction pour certains élèves à la centaine.

Les grilles de 99 comportent un zéro et n'ont pas de numéro à trois chiffres. Chaque ligne commence par un multiple de dix au lieu de se terminer par un multiple de dix.

Il y a de bien meilleures fiches d'exercices sur la page de fiches d'exercices des droites numériques.

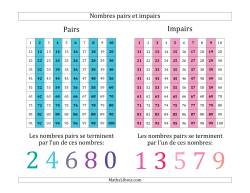
Distinguer les nombres pairs des nombres impairs est une compétence importante que les jeunes étudiants doivent apprendre. Le vocabulaire des nombres pairs et impairs est utilisé tout au long de leur éducation mathématique, il est donc nécessaire de l'apprendre le plus tôt possible. Le fait de relier des cubes peut être très utile pour démontrer visuellement les nombres pairs et impairs. Créez les nombres de 1 à 10 (ou plus) en utilisant des cubes de connexion par paires et les élèves verront rapidement que les nombres impairs ont un cube non apparié qui peut être considéré comme le "cube impair". Une fois qu'ils auront vu ce modèle, ils pourront peut-être l'étendre sans faire de modèles de cubes. Demandez-leur ce qu'il en est de 11, 12, 35, etc.

Maintenant, voyons si les élèves peuvent écrire les chiffres qui sont écrits ! Les fiches d'exercices sur la lecture des chiffres écrits en mots ne comportent pas d'options de format car les feuilles de questions des élèves sont toutes écrites en mots. Les corrigés sont formatés avec un séparateur de milliers comnme virgules si nécessaire.

Il s'agit de la "vieille école" la plus ancienne possible. Enfilez votre tunique et ramassez votre scutum pour vous attaquer aux fiches d'exercices sur les chiffres romains. Vous trouverez ci-dessous des options pour les formes standard et compacts. La forme standard des fiches d'exercices en chiffres romains comprend des chiffres dans la version communément enseignée où 999 est CMXCIX (c'est-à-dire que le chiffre est écrit une valeur à la fois). Les versions compactes sont destinées à ceux qui souhaitent une version plus complexe où les chiffres romains sont écrits de manière aussi concise que possible. Dans la version compacte, 999 est écrit comme IM (c'est-à-dire un de moins que 1000).

Le système de numération binaire a des applications larges, mais il est surtout connu pour sa prédominance dans l'architecture informatique. Apprendre le système binaire encourage non seulement une réflexion d'ordre supérieur, mais il prépare également les élèves pour des études futures les mathématiques et l'informatique. Le tableau ci-dessous peut être être utile pour les élèves qui ont besoin d'aide pour aligner les choses et l'apprentissage de la valeur positionnelle en ce qui concerne le système binaire. Nous avons inclus une colonne de nombre de base 10, donc vous pouvez utiliser le tableau pour la conversion entre systèmes décimaux et binaires.

L'astuce du nombre mystère ci-dessous est en fait basée sur des nombres binaires. Comme vous le savez, chaque endroit dans le système binaire est une puissance de 2 (1, 2, 4, 8, 16, etc..). Étant donné que chaque nombre décimal (base 10) peut être exprimé comme un nombre binaire, chaque nombre décimal peut donc être exprimé comme une somme d'un ensemble unique de puissances de 2. C'est cette conception qui rend cette astuce fonctionnelle. Vous pouvez remarquer que le plus grand nombre décimal sur les cartes est 63 qui est également le plus grand nombre à 6 chiffres (111111). La position de la cible sur chaque version de l'astuce du numéro mystère contient les puissances de 2 associées avec les premières valeurs de 6 places dans le système binaire (1, 2, 4, 8, 16, 32). Chacune des 6 cartes représente une valeur de position spécifique. Tous les 32 nombres sur chaque carte contiennent un 1 dans le lieu associé quand au format binaire. Fondamentalement, quand «l'ami(e)» identifie les cartes qui contiennent le nombre mystère, ils vous donnent un nombre binaire qui doit simplement convertir un nombre décimal. Juste pour le plaisir, nous avons mélangé les nombres sur les cartes et la position de la cible sur les versions C à J. Version A comprend les nombres dans l'ordre croissant et version B comprend les nombres dans l'ordre décroissant. Les autres versions (B à J) seront disponibles une fois que vous cliquez sur la version A ci-dessous.