Fiches d'Exercices sur la Multiplication Posée

Fiches d'exercices de multiplication posée comprenant une variété de tailles de nombres et des options pour différents formats de nombres.

Il n'y a pas mille séparateurs dans les nombres sur les premières feuilles de calcul. Cela rend la lecture des nombres un peu plus difficile, mais il est parfois préférable de ne pas avoir trop de choses qui gênent lorsque les élèves apprennent de longues multiplications. Les corrigés incluent des réponses avec les étapes indiquées, afin que les étudiants et les enseignants puissent diagnostiquer tout problème dans les étapes qu'ils ont suivies pour répondre aux questions. Les réponses utilisent un algorithme papier-crayon couramment utilisé aux États-Unis et dans d'autres pays.

Les virgules sont incluses comme séparateurs de milliers pour les nombres sur les fiches d'exercises suivantes. Les virgules sont utilisées aux États-Unis et dans d’autres pays anglophones pour faciliter la lecture des chiffres. Comme pour les autres fiches d'exercises de multiplication sur cette page, les corrigés incluent les étapes.

Separating thousands with spaces avoids any confusion with commas and periods. Various number formats in different countries and languages use commas and periods for both decimals and thousand separators, but a space is only ever used as a thousands separator. It is more common in some countries such as Canada and France, but it is being adopted more in other parts of the world.

À certains endroits, les points sont utilisés comme séparateurs de milliers et les virgules comme séparateurs décimaux. C'est très déroutant pour les personnes habituées aux chiffres au format américain.

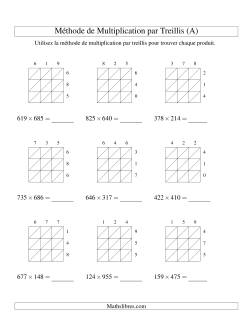
La méthode de multiplication par trellis ou par tamis, est une excellente stratégie pour les élèves à utiliser pour calculer les problèmes de Multiplication Posée sur le crayon et le papier. Nous avons fait la première étape de la préparation d'un treillis facile comme les fiches de calcul ci-dessous qui ont leur garphique prédessiné. Avec un peu de pratique, les élèves peuvent utiliser un papier millimétré ou dessiner leurs propres grilles à la main. Le premier facteur est séparé par la valeur d'endroit le long du dessus du treillis, valorisant chaque endroit sa propre colonne. Le deuxième facteur est séparé de la même manière, mais le long du côté droit avec une valeur d'endroit par ligne. Les numéros de lignes et colonnes à un seul chiffre sont multipliés ensemble et leur produit est écrit dans la case correspondante, en séparant les locaux des dizaines et unités de chaque côté de la diagonale. Enfin, les « lignes » diagonales sont résumés et regroupés à partir de la diagonale dans le coin inférieur droit qui aura seulement un seul chiffre dedans. Les clés de la réponse que nous avons fourni devraient vous donner une bonne idée de comment accomplir la méthode de multiplication par treillis comme un pro. Une fois que les élèves ont un peu de pratique, vous trouverez peut-être que c'est leur méthode préférée pour le calcul des produits d'un grand nombre. Cette méthode est hautement évolutive, ce qui signifie que c'est une tâche simple à multiplier un chiffre de 10 par un numéro à 10 chiffres, etc...

La propriété distributive de la multiplication permet aux élèves de « diviser » les facteurs en additions pour faciliter la multiplication. Cela aide également les élèves à apprendre à effectuer la multiplication mentalement plutôt qu'en utilisant des méthodes papier et crayon. Souvent, les nombres sont divisés par valeur de position, donc 123 devient 100 + 20 + 3. Si l'on voulait multiplier 123 par 4, vous pourriez multiplier 100 par 4, 20 par 4 et 3 par 4 pour obtenir 400, 80 et 12, ce qui donne 492. Si vous multipliez un nombre à plusieurs chiffres par un nombre à plusieurs chiffres, vous pouvez diviser les deux nombres en valeurs de position ajoutées. Par exemple, 938 × 74 = (900 + 30 + 4) × (70 + 4) = (900 × 70) + (900 × 4) + (30 × 70) + (30 × 4) + (8 × 70) + (8 × 4) = 63 000 + 3 600 + 2 100 + 120 + 560 + 32 = 69 412. Toutes les fiches d'exercices de cette section contiennent une question modèle. Bien sûr, il pourrait être plus facile de répondre à des questions avec des nombres plus grands en utilisant la multiplication par cases.

La multiplication sur du papier millimétré aide les élèves à « aligner » leurs nombres lorsqu'ils répondent à des questions de multiplication posée. Ces fiches d'exercices incluent des grilles personnalisées qui offrent suffisamment d'espace pour une question.

Si vous ou vos élèves souhaitez créer vos propres questions, ces fiches d'exercises vierges devraient accélérer le processus.

La stratégie de réduction de moitié et de doublement est accomplie à peu près de la même manière que son nom. Il suffit de diviser par deux un nombre et de doubler l'autre, puis de multiplier. Dans de nombreux cas, cela rend la multiplication de deux nombres plus facile à accomplir mentalement. Cette stratégie n'est pas adaptée à tous les problèmes de multiplication, mais elle fonctionne certainement bien si certains nombres sont impliqués. Par exemple, doubler un 5 donne un 10 que la plupart des gens auraient plus de facilité à multiplier. Bien sûr, cela dépendrait de la réduction de moitié de l'autre facteur. 5 × 72, en utilisant la stratégie de réduction de moitié et de doublement (doubler le premier nombre et diviser par deux le second dans ce cas) donne 10 × 36 = 360. La pratique des feuilles de travail de cette section aidera les élèves à se familiariser avec les cas dans lesquels cette stratégie serait utilisé.

Multiplication de systèmes de numération en diverses bases comprenant des nombres binaires, ternaires quaternaires, quinaires, sénaires, octaux, duodécimaux, hexadécimaux, vigésimaux et hexatrigémaux.